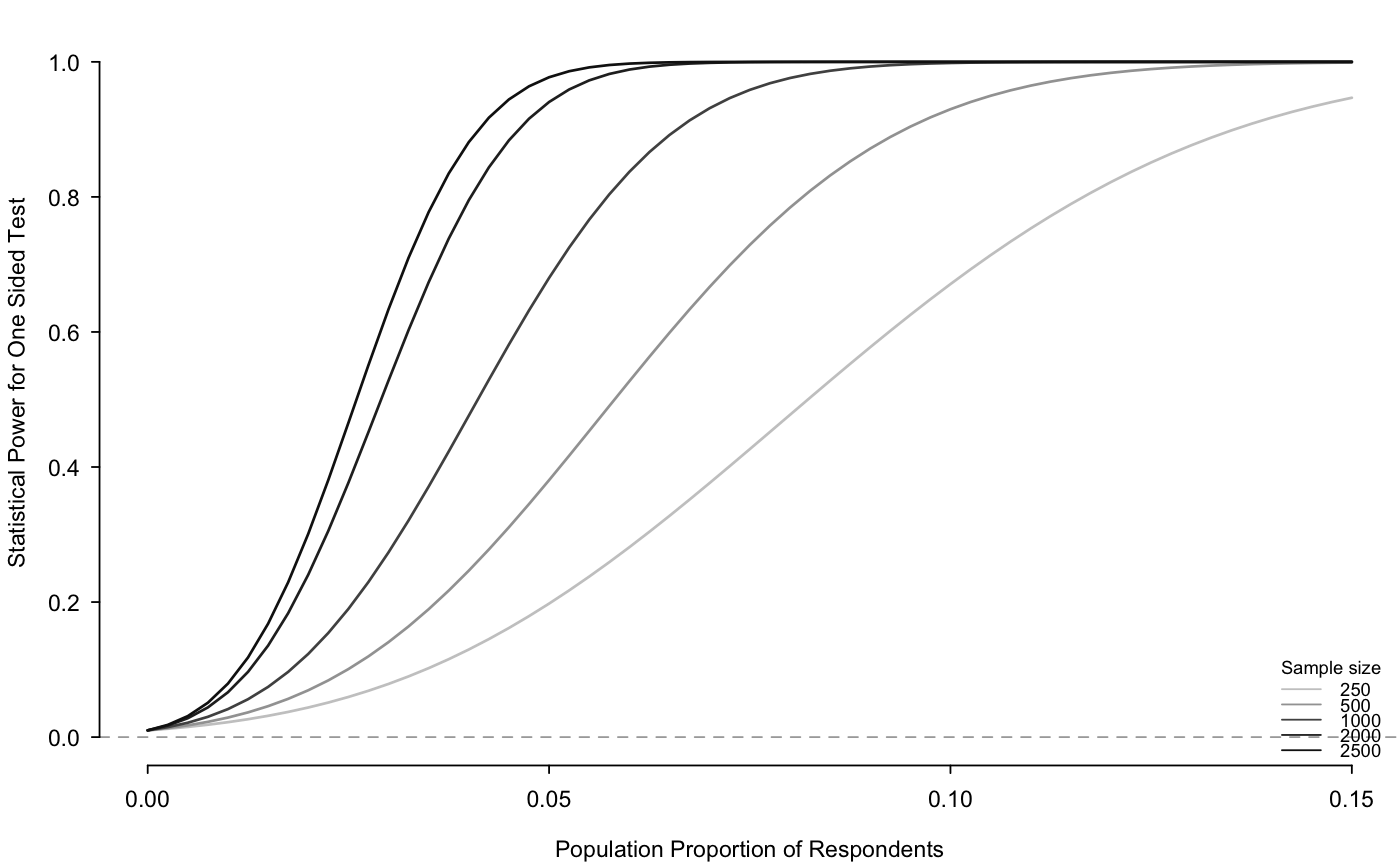
Power Analysis Plot for Randomized Response

power.rr.plot generates a power analysis plot for randomized response survey designs.

power.rr.plot(p, p0, p1, q, design, n.seq, r, presp.seq, presp.null =
NULL, sig.level, prespT.seq, prespC.seq, prespT.null = NULL, prespC.null,
type = c("one.sample", "two.sample"), alternative = c("one.sided",
"two.sided"), solve.tolerance = .Machine$double.eps, legend = TRUE, legend.x
= "bottomright", legend.y, par = TRUE, ...)

Arguments

p

The probability of receiving the sensitive question (Mirrored Question Design, Unrelated Question Design); the probability of answering truthfully (Forced Response Design); the probability of selecting a red card from the 'yes' stack (Disguised Response Design).
p0

The probability of forced 'no' (Forced Response Design).
p1

The probability of forced 'yes' (Forced Response Design).
q

The probability of answering 'yes' to the unrelated question, which is assumed to be independent of covariates (Unrelated Question Design).
design

Call of design (including modified designs) used: "forced-known", "mirrored", "disguised", "unrelated-known", "forced-unknown", and "unrelated-unknown".
n.seq

A sequence of number of observations or sample sizes.
r

For the modified designs only (i.e. "forced-unknown" for Forced Response with Unknown Probability and "unrelated-unknown" for Unrelated Question with Unknown Probability), r is the proportion of respondents allocated to the first group, which is the group that is directed to answer the sensitive question truthfully with probability p as opposed to the second group which is directed to answer the sensitive question truthfully with probability 1-p.
presp.seq

For a one sample test, a sequence of probabilities of possessing the sensitive trait under the alternative hypothesis.
presp.null

For a one sample test, the probability of possessing the sensitive trait under the null hypothesis. The default is NULL meaning zero probability of possessing the sensitive trait.
sig.level

Significance level (Type I error probability).
prespT.seq

For a two sample test, a sequence of probabilities of the treated group possessing the sensitive trait under the alternative hypothesis.
prespC.seq

For a two sample test, a sequence of probabitilies of the control group possessing the sensitive trait under the alternative hypothesis.
prespT.null

For a two sample test, the probability of the treated group possessing the sensitive trait under the null hypothesis. The default is NULL meaning there is no difference between the treated and control groups, specifically that prespT.null is the same as prespC.null, the probability of the control group possessing the sensitive trait under the null hypothesis.
prespC.null

For a two sample test, the probability of the control group possessing the sensitive trait under the null hypothesis.
type

One or two sample test. For a two sample test, the alternative and null hypotheses refer to the difference between the two samples of the probabilities of possessing the sensitive trait.
alternative

One or two sided test.
solve.tolerance

When standard errors are calculated, this option specifies the tolerance of the matrix inversion operation solve.
legend

Indicator of whether to include a legend of sample sizes. The default is TRUE.
legend.x

Placement on the x-axis of the legend. The default is "bottomright".
legend.y

Placement on the y-axis of the legend.
par

Option to set or query graphical parameters within the function. The default is TRUE.
...

Additional arguments to be passed to par()

Details

This function generates a power analysis plot for randomized response survey designs, both for the standard designs ("forced-known", "mirrored", "disguised", "unrelated-known") and modified designs ("forced-unknown", and "unrelated -unknown"). The x-axis shows the population proportions with the sensitive trait; the y-axis shows the statistical power; and different sample sizes are shown as different lines in grayscale.

References

Blair, Graeme, Kosuke Imai and Yang-Yang Zhou. (2014) "Design and Analysis of the Randomized Response Technique." Working Paper. Available at http://imai.princeton.edu/research/randresp.html.

Examples


## Generate a power plot for the forced design with known 
## probabilities of 2/3 in truth-telling group, 1/6 forced to say "yes" 
## and 1/6 forced to say "no", varying the number of respondents from 
## 250 to 2500 and the population proportion of respondents 
## possessing the sensitive trait from 0 to .15.


presp.seq <- seq(from = 0, to = .15, by = .0025)
n.seq <- c(250, 500, 1000, 2000, 2500)
power.rr.plot(p = 2/3, p1 = 1/6, p0 = 1/6, n.seq = n.seq,
              presp.seq = presp.seq, presp.null = 0,
              design = "forced-known", sig.level = .01,
              type = "one.sample",
              alternative = "one.sided", legend = TRUE)
				       
    
## Replicates the results for Figure 2 in Blair, Imai, and Zhou (2014)